2020-01-29

肺炎系列 (三十) 數學圖表課


為何我每天要收集官方數據，然後畫圖表呢？

我嘗試用數學方法，監察和預測肺炎情況。
有人說，由2020-1-10的頭兩個星期，確診病例以拋物線或Exponential 式不斷向上地增加 [註一和二]。我有些同意，也有些不同意...

   

拋物線 Parabola

y = x²
f(x)=ax²+bx+c
[註三]

指數成長 Exponential growth

y = abx
[註四]

雖然確診病例在頭兩個星期，好像以拋物線或Exponential 式不斷向上，但是現實上不可能無限地增加。歷史告訴我們，疫情總有冷卻的一天，問題是需要幾多時間，和要有幾多人受影響。

流感 Influenza

看看每年的嚴重流感病例數字，以下的圖表來自香港衞生署衞生防護中心的刊物，每年都有一次流感高峰期，在上山的時候，感到很斜很害怕。疫情總有山頂的時候，然後回落 [註六]。

題外話，2017年，有人說又有夏季流感高峰期，望真一點，其實是平時冬季的山峰，延遲到夏季才出現 [註六]，這就是查看圖表數據的重要性，fact check。


   

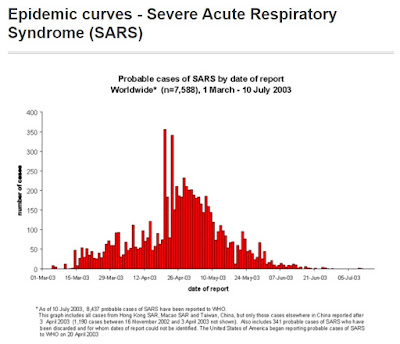
沙士 SARS

[註七 WHO]

當年香港，花了3個多月對抗SARS疫情，瀝瀝在目、刻骨銘心。

   

乙狀曲線 Sigmoid curve - 邏輯函數增長 Logistic Growth

[註八]

[註九至十]
(Pierre François Verhulst 在1838年至1847年的三篇論文中開發了logistic function [註十一])

我每天要收集官方數據，然後畫圖表，就是希望有一天疫情像乙狀的減慢、平穩的「勢頭」 [註十二]。才有望等到回落的時候，再估計隔離和戴口罩的日子。

當年很沉悶的函数數學課，二十多年後的今天，終於養兵8942日 (24.5年)，用在一晚，哈。

  

總結

學海無涯，回頭是岸。

祈求新型冠狀病毒感染的肺炎，新年快落。

  

參考資料

[註一] 國家健康衞生委員會 - 疫情通報
[註二] 香港衞生署衞生防護中心
發佈者： 於
標籤： ,

沒有留言:

發佈留言

訂閱： 發佈留言 (Atom)